写在前面
代码开发使用的运行环境是python 3.6.1的版本,配合vscode+ananconda的代码编写环境进行相关的代码编写任务,代码运行所需要的库及对应版本如下:
# Name Version
numpy 1.13.1
pandas 0.23.4
如果相关运行环境没有搭建可以参考我的另一篇文章机器学习环境搭建(Ananconda +VScode) – 掘金 (juejin.cn)
1. 算法简要介绍
在机器学习当中主要分为三类,一类是监督学习,一类是无监督学习,剩下的另一类则是强化学习,而接下要讲的k-邻近算法则是属于机器学习当中监督学习一类的。
K近邻(K-Nearest Neighbor, KNN)是一种最经典和最简单的有监督学习方法之一。K-近邻算法是最简单的分类器,没有显式的学习过程或训练过程,是懒惰学习(Lazy Learning)。当对数据的分布只有很少或者没有任何先验知识时,K 近邻算法是一个不错的选择。
K近邻算法既能够用来解决分类问题,也能够用来解决回归问题。该方法有着非常简单的原理:当对测试样本进行分类时,首先通过扫描训练样本集,找到与该测试样本最相似的个训练样本,根据这个样本的类别进行投票确定测试样本的类别。也可以通过个样本与测试样本的相似程度进行加权投票。如果需要以测试样本对应每类的概率的形式输出,可以通过个样本中不同类别的样本数量分布来进行估计。
k-近邻算法一般实现步骤如下:
- 收集数据: 可以使用任何方法。
- 准备数据: 距离计算所需要的数值,最好时结构化的数据格式。
- 分析数据: 使用Matplotlib画二维扩散图
- 测试算法: 计算错误率
- 使用算法: 首先需要输入样本数据和结构化的输出结果,然后运行k-邻近算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理
2. 原理阐述
2.1 核心思想
在上面算法简述当中,其实我们可以知道k邻近核心思想非常简单即给定测试样本,然后基于某种距离度量找出训练集中与其最靠近的k个样本,然后基于这k个样本的信息来进行预测。通常在进行分类任务时,是选择k个样本中出现最多的类别标记作为预测结果。总结起来就是“近朱者赤,近墨者黑”。

在上面的图片中,共有三种图形,其中三角形和矩形代表训练集中不同的类别标签,而圆形则是代表需要进行预测的数据
从图上我们可以知晓对于不同k和距离预测的结果也是不一样。
从上面的描述当中,其实我们可以知道,在k邻近算法预测结果是否准确与两个关键元素分不开,即距离度量和k值,其中如何进行距离度量是整个算法实现的关键,那接下来继续说说常见的距离度量方式和k值选取。
2.2 常见的距离度量
– 欧式距离
在所有距离度量中,欧式距离是我们最常接触的距离度量方式,衡量的是空间中两点的绝对距离,也是最简单实现的一种。公式如下
d=∑i=1n(xi−yi)2begin{aligned}
d = sqrt[]{sum_{i=1}^n (x_i-y_i)^2}
end{aligned}
在上述公式中xix_i代表训练集中数据的每个特征值,yiy_i代表的是测试集中数据的每个特征值
– 曼哈顿距离
上面的欧式距离虽然是我们最常见的距离度量方式,但是它也有明显的缺陷——只能度量两点的直线距离,但是在现实世界当中,我们不可能直接从起点到达终点,而曼哈顿距离考虑到了这一点,因此,曼哈顿距离也是我们比较常见一种距离度量的方式,其公式如下
d=∑i1n∣xi−yi∣begin{aligned}
d = sum_{i_1}^n | x_i – y_i |
end{aligned}
在上述公式中xix_i代表训练集中数据的每个特征值,yiy_i代表的是测试集中数据的每个特征值
– 闵可夫斯基距离
除了上述的欧式距离和曼哈顿距离外还有闵可夫斯基距离,闵可夫斯基距离不是一种距离,而是一组距离的定义。对应Lp范数,p为参数。
闵氏距离的定义:两个n维变量(或者两个n维空间点)x1(x11,x12,…,x1n)与 x2(x21,x22,…,x2n)间的闵可夫斯基距离定义为:
d=∑i=1n∣xi−yi∣ppbegin{aligned}
d = sqrt[p]{sum_{i=1}^n |x_i – y_i|^p}
end{aligned}
其中p是一个变参数。
当p=1时,就是曼哈顿距离,
当p=2时,就是欧氏距离,
根据变参数的不同,闵氏距离可以表示一类的距离。
2.3 k值的选定
在k近邻算法中除了距离度量的选取会影响到最终结果外,k值的选定也起着非常重要的作用,不同的k值可能会有不同的预测结果。 因此,在实际算法实现的过程中,我们一般是将k值选为奇数,例如1,3,5等等这样的数,这样做得目的是为了防止训练集中出现两个点与要进行预测的点的距离相同时,算法无法界定那个更合适,而给出错误预测结果。
同时要指出的是k值选定,不宜过大或是过小。
如果选择较小的k值,预测结果会对近邻的点非常敏感,如果这个近邻的点恰恰是个噪声点,那么分类就会出错。
如果选择较大的k值,比如说等于两类数目之和,那么哪个类数目多,这个点就会被分到哪个类。
3. 算法代码实现
3.1 开始前言
实现k邻近算法所用的来自于kaggle平台鸢的尾花数据集 Kaggle: Your Machine Learning and Data Science Community,

3.2 数据准备
在读取数据集中数据数据的过程中,由于数据集是.csv格式的文件,因此使用pandas库中的函数进行数据读取

数据获取完整片段
# 数据准备
def getData(path):
names = ['sepal_length','sepal_width','petal_length','petal_width','species']
# 使用pandas中的函数读取.csv文件
trains = pd.read_csv(path,header=0,names=names)
mat = zeros((len(trains),4)) # 生成len(trains) * 4的矩阵
index = 0
label = [] # 存储标签
for i in range(len(trains)):
label.append(trains[names[-1][i]])
mat[index:] = trains[names[0:4]]
return norm(mat),label
3.3 数据归一化处理
在正式进行距离度量之前,我们首先要进行归一化的处理,这是因为在数据集稍微大一点的机器学习当中,数据的分布并不是绝对平均,总是会存在一部分数据偏离过大或是过小,这样会对算法预测造成一定的干扰,影响预测的结果。
而归一化将取值范围处理为0到1之间可以将这些影响尽可能的消除,所以在实现任何机器学习算法时,都要先将进行数据归一化操作。
归一化的公式如下
newValue=(oldValue−min)/(max−min)begin{aligned}
newValue = (oldValue – min)/(max – min)
end{aligned}
其中min和max代表数据集中的最大特征值和最小特征值
上述的归一化公式可以将数据的取值范围处理为0到1之间
数据归一化处理完整片段
# 数据归一化处理
def norm(Mat):
# 获取每一列的最大最小值,返回一个矩阵
min_type = Mat.min(0)
max_type = Mat.max(0)
different = max_type - min_type
newMat = zeros(Mat.shape)
newMat = Mat - tile(min_type,(Mat.shape[0],1))
newMat = newMat/tile(different,(Mat.shape[0],1))
print(len(Mat))
print(len(newMat))
return newMat
归一化结果:

3.4 对数据进行距离度量
距离度量是整个k近邻算法最重要的一步,不同的距离度量方式可能导致不同的结果,在这段距离度量的代码当中采取的是欧式距离,函数的参数是训练集和测试集,返回的是测试集到训练集从小到大的距离的矩阵索引,代码如下
距离度量完整片段
# 距离计算
def distance(goalSet,dataSet):
# 获取测试集的一维数组长度
dataSetSize = dataSet.shape[0]
# 复制copygoal,返回datasetSize行1列的数组
copygoal = tile(goalSet,(dataSetSize,1))
# 开始计算当前点与已知数据集的点的距离
diffMat = copygoal - dataSet
powdiffMat = diffMat**2
diffMat = powdiffMat.sum(axis=1) #按行求和
Mat = diffMat**0.5
# 获取数组从小到达的索引(数组下标)
sortedDistance = Mat.argsort()
return sortedDistance
距离度量结果:

3.5 数据特征预测
在完成前面的步骤之后,这一步就非常简单了,这一步只是在简单的统计前k个数据对应标签出现的次数,然后返回出现次数最多的标签。
在该函数当中共有四个参数,分别是需要进行预测的数据,训练集的特征矩阵,训练集的标签矩阵以及K值,最后结果返回预测的结果
数据特征统计完整片段
# k近邻算法核心实现
def classfy0(inX, dataSet, labels, k):
# 距离计算(欧式距离)
sortedDistance = distance(inX,dataSet)
classcount = {}
# 统计距离当前点最近的k个标签的个数
for i in range(k):
Visable = labels[sortedDistance[i]]
classcount[Visable] = classcount.get(Visable,0) + 1
# 对统计出的标签数从小到大排序
sortedClassnumber = sorted(classcount.items(),
key=operator.itemgetter(1),reverse=True)
# 返回预测值
return sortedClassnumber[0][0]
3.6 算法测试
# 算法测试
def testClass(textPro,k):
# 统计错误个数
erroConut = 0.0
group,label = getData(os.path.dirname(os.path.abspath(__file__)) + "\IRIS.csv")
# group,label = createDateSet()
textSize = int(textPro*group.shape[0])
for i in range(textSize):
textresult = classfy0(group[i,:],group[textSize:group.shape[0]],label[textSize:group.shape[0]],k)
print("预测结果:%s,真实结果:%s" % (textresult,label[i]))
if (textresult != label[i]):
erroConut += 1.0
print("错误次数:%d " % erroConut)
print("错误百分比:%f %%" % (erroConut/textSize*100))
数据集划分按照4:6划分测试集和训练集,下面是对于不同的k值,k近邻算法的预测能力
预测结果:
k=3时算法的预测能力

k=5时算法的预测能力

k=25时算法的预测能力

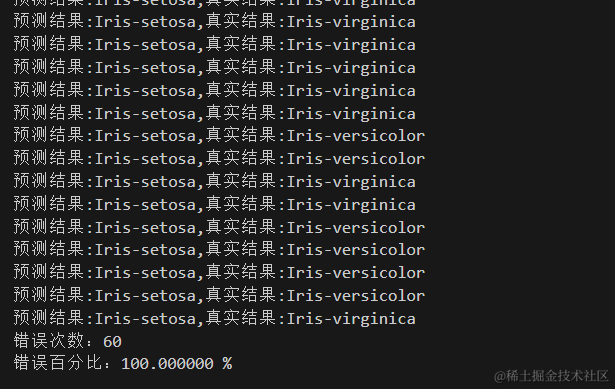
k=60时算法的预测能力

3.6.1 结果分析
从上面的预测结果可以看到当k取值在5附近时,k邻近的预测准确率是比较高的,但是往后k值越大,准确率反而下降。
选择较小的K值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
选择较大的K值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。
4. 算法实现过程中遇到的问题及总结
4.1 问题及解决方法
1> 算法实现初期,错误率过高

原因:
这是因为选择的鸢尾花数据集太小,相同数据都是分布在一起的,导致在最后进行测试集和训练集划分的时候划分不均匀,相似数据都划分到一块
解决方法:
将原始数据集打乱,使得相似数据分散,不集中。
2> 文件读取方式有误,导致读取的数据总是多出符号
原因: 由于数据集是使用的.csv格式的文件,正常通过open,read的方式读取然后分割数据会多出‘,’
解决方法: 获取数据的方式改为使用pandas库中的red_csv函数可以有效解决这个问题。
4.2 总结
knn算法优缺点
优点:
- 简单,易于理解,无需建模与训练,易于实现;
- 适合对稀有事件进行分类.
- 由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属的类别,因此对于类域的交叉或重叠较多的待分类样本集来说,KNN方法较其他方法更为适合
- 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量比较小的类域采用这种算法比较容易产生误分类情况
缺点:
- 计算量大,尤其是特征数非常多的时候
- 样本不平衡的时候,对稀有类别的预测准确率低
- 是慵懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
5. 补充
完整数据集和代码下载地址: machine/knn · 麻瓜啃大瓜/机器学习 – 码云 – 开源中国 (gitee.com)
交叉验证(未完善)

